In abstract algebra, finite group theory is in its core. Now from Lagrange theorem, we have
Lemma 1 Let ![]() be a subgroup of a finite group
be a subgroup of a finite group ![]() . Then the order of
. Then the order of ![]() is a divisor of the order of
is a divisor of the order of ![]() .
.
This theorem states the necessary condition for a finite group ![]() to be a subgroup of a finite group
to be a subgroup of a finite group ![]() . But it does not give us the sufficient condition for a finite group to be a subgroup of another finite group. i.e. the converse is false.
. But it does not give us the sufficient condition for a finite group to be a subgroup of another finite group. i.e. the converse is false.
For example, given alternating group ![]() of order
of order ![]() , there does not exist a subgroup of order
, there does not exist a subgroup of order ![]() . (The proof of this part will be remained to the reader.)
. (The proof of this part will be remained to the reader.)
Suppose that the order of a finite group is ![]() , how do we know whether there exists a subgroup of order a divisor of
, how do we know whether there exists a subgroup of order a divisor of ![]() ? Sylow Theorems give the answer.
? Sylow Theorems give the answer.
There are in fact three theorems in the set of Sylow Theorems. Let us state them one by one
Theorem 1 (First Sylow Theorem) Let ![]() be a finite group and let
be a finite group and let ![]() where
where ![]() and where
and where ![]() does not divide
does not divide ![]() . Then
. Then
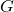 contains a subgroup of order
contains a subgroup of order 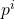 for each
for each 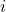 where
where 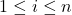 .
.- Every subgroup
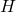 of
of 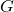 of order
of order 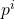 is a normal subgroup of a subgroup of order
is a normal subgroup of a subgroup of order 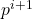 for
for 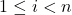 .
.
Before stating the Second Sylow Theorem, we require some terminology right now.
Definition 1 A ![]() -group is a group such that each element in the group has order a power of
-group is a group such that each element in the group has order a power of ![]() .
.
Definition 2 A Sylow ![]() –subgroup
–subgroup ![]() of a group
of a group ![]() is a maximal
is a maximal ![]() -subgroup of G, that is, a
-subgroup of G, that is, a ![]() -subgroup contained in no larger
-subgroup contained in no larger ![]() -subgroup.
-subgroup.
Now we continue with the Second Sylow Theorem.
Theorem 2 (Second Sylow Theorem) Let ![]() and
and ![]() be Sylow
be Sylow ![]() -subgroups of a finite group
-subgroups of a finite group ![]() . Then
. Then ![]() and
and ![]() are conjugate subgroups of
are conjugate subgroups of ![]() .
.
Theorem 3 (Third Sylow Theorem) If ![]() is a finite group and
is a finite group and ![]() divides
divides ![]() then the number of Sylow
then the number of Sylow ![]() -subgroups is congruent to
-subgroups is congruent to ![]() modulo
modulo ![]() and divides
and divides ![]() .
.
As the Second and Third Sylow Theorem are quite complex, and our main focus would be finding the converse of Lagrange theorem, so we will only delve into the First Sylow Theorem.
Proof and idea. We use induction in proving this theorem. As by Cauchy theorem, there exists a subgroup of order ![]() . If we can use induction on the power of
. If we can use induction on the power of ![]() , then we are done.
, then we are done.
As Sylow Theorem is highly related to the concept of cosets and normalizer group, we can consider the group ![]() , which we denote as normalizer of
, which we denote as normalizer of ![]() in
in ![]() .
.
Lemma 2 Let ![]() be a
be a ![]() -subgroup of a finite group
-subgroup of a finite group ![]() . Then
. Then
![]()
Continuing our proof, as ![]() is a normal subgroup of
is a normal subgroup of ![]() , we can form the factor group
, we can form the factor group ![]() . Suppose that this factor is of order power of
. Suppose that this factor is of order power of ![]() , then by Cauchy theorem again, there exists a subgroup
, then by Cauchy theorem again, there exists a subgroup ![]() of order
of order ![]() , and using canonical homomorphism we could proceed our induction.
, and using canonical homomorphism we could proceed our induction.
Let ![]() be a subgroup of order
be a subgroup of order ![]() , where
, where ![]() , so
, so ![]() divides
divides ![]() . By Lemma 2, we derive that
. By Lemma 2, we derive that ![]() divides
divides ![]() . Therefore the factor group
. Therefore the factor group ![]() has a subgroup
has a subgroup ![]() of order
of order ![]() .
.
Consider the canonical homomorphism
![]()
Then ![]() has order
has order ![]() . Thus our proof is complete. The second part follows immediately from part 1.
. Thus our proof is complete. The second part follows immediately from part 1.
Applications
Proposition 1 No group of order ![]() for
for ![]() is simple.
is simple.
Proposition 2 No group ![]() of order
of order ![]() is simple.
is simple.
Proof. By the First Sylow Theorem, ![]() has a Sylow
has a Sylow ![]() -subgroup. Also, by the Third Sylow Theorem, the number of such Sylow
-subgroup. Also, by the Third Sylow Theorem, the number of such Sylow ![]() -subgroups of
-subgroups of ![]() is
is ![]() and is a divisor of
and is a divisor of![]() . So the number of such subgroups is
. So the number of such subgroups is ![]() . As the only Sylow
. As the only Sylow ![]() -subgroup, it must be a normal subgroup of
-subgroup, it must be a normal subgroup of ![]() . Thus
. Thus ![]() is not simple.
is not simple.
Leave a Reply