Chapter 1: Motivation for Measure Theory
As the first chapter of this series, we begin by presenting the motivation behind measure theory.
Motivation
Measure theory was developed to address the limitations of Riemann integration. Let’s first recall Riemann integration, which approximates the integral through upper and lower bounds, taking the limit as the partition becomes infinitely fine. However, this approach fails for certain special functions. For example:
No matter how we partition the interval, one segment always yields infinity. Yet through improper integration, we know this area can be calculated. Another famous example is the Dirichlet function:
In any interval, the supremum is always 1 and the infimum 0, making the upper and lower limits unequal. Measure theory extends integrability to such functions by optimizing how we partition integration domains.
Measure
When integrating, we approximate functions using sums of small rectangles, whose lengths and widths determine the integral’s definition. This necessitates a generalized notion of “length” beyond intervals.
We first consider properties of subsets of ℝ. For intervals, the natural measure is the difference between endpoints. If we define μ as such a function, clearly: ![]() where open intervals can be replaced with any interval type. Our goal is to define set “length” through open intervals because of their nice properties under countable unions/intersections. We call this generalized length a “measure”
where open intervals can be replaced with any interval type. Our goal is to define set “length” through open intervals because of their nice properties under countable unions/intersections. We call this generalized length a “measure” ![]() , requiring:
, requiring:
- Translation invariance:
![Rendered by QuickLaTeX.com \[\mu(t + A) = \mu(A)\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-9428c43c044da6803551523d4d8482d4_l3.png)
-
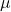 is defined on all subsets of
is defined on all subsets of 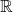 with
with  (non-negativity)
(non-negativity) 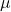 agrees with interval lengths as above.
agrees with interval lengths as above.- Countable additivity:
![Rendered by QuickLaTeX.com \[\mu\left(\bigcup_{k=1}^{\infty} A_k\right) = \sum_{k=1}^{\infty} \mu(A_k)\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-5533291d5d51a8f5eb1c530cf728c4be_l3.png)
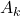
However, no such function satisfies all four properties simultaneously (as shown by Vitali’s construction involving rational/irrational sets). We therefore relax condition (1), allowing μ to be defined only on special subsets.
σ-Algebra
We abstractly define measure on a collection S of subsets of X called a σ-algebra, requiring:
![Rendered by QuickLaTeX.com \[\emptyset \in S\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-d27be52f20caf16de6113854e7dc23c4_l3.png)
- Closed under complements:
![Rendered by QuickLaTeX.com \[E \in S \Rightarrow X\setminus E \in S\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-0fe959c842a7f4e5376fa55069fb6387_l3.png)
- Closed under countable unions:
![Rendered by QuickLaTeX.com \[\bigcup_{k=1}^{\infty} E_k \in S\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-66df71dfc3c3b24d523b9cf19ee48c1f_l3.png)
Key benefits:
- We can define
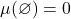
- Enables measure definition for complements and countable intersections (via De Morgan’s laws)
- Provides the foundation for limit operations
Borel Sets*
From topology, we naturally consider measures on ℝ’s open sets. The smallest σ-algebra containing all open sets is the Borel σ-algebra. Its sets are generated through countable operations on open intervals, including all closed sets. Crucially, we can define a well-behaved measure μ on Borel sets satisfying countable additivity.
Concretely, for a Borel set A, we define:
![Rendered by QuickLaTeX.com \[\mu(A) = \inf \{ \sum_{k=1}^{\infty} \mu(I_k) : A \subseteq \bigcup_{k=1}^{\infty} I_k, \text{ } I_k \text{ open intervals} \}\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-1705522d21a05fde56cbf66bdc866a72_l3.png)
This means we cover A with open intervals and take the infimum of their total lengths, extending our measure from intervals to Borel sets.
![Rendered by QuickLaTeX.com \[f(x) = \begin{cases} \frac{1}{\sqrt{x}} & \text{if } 0 < x \leq 1, \\ 0 & \text{if } x = 0.\end{cases}\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-1d601579abb01b21def1a1364677a494_l3.png)
![Rendered by QuickLaTeX.com \[f(x) =\begin{cases} 1 & \text{if } x \text{ is rational}, \\ 0 & \text{if } x \text{ is irrational}.\end{cases}\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-e968807978b6634321320874e45627dc_l3.png)
Leave a Reply