An inequality problem

June 2026
M	T	W	T	F	S	S
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

Let $f$ be a continuous integrable real function on $[0,1]$ , then

$\int_{0}^{1} e^{f(x)} dx \cdot \int_{0}^{1} e^{-f(y)} dy \geq 1$

Solution 1

By Cauchy-Schwarz inequality,

$\begin{align*} \int_{0}^{1} e^{f(x)} dx \cdot \int_{0}^{1} e^{-f(y)} dy &\geq \left(\int_{0}^{1} e^{f(x) - f(x)} dx\right)^2 \\ &= \left(\int_{0}^{1} 1 \, dx\right)^2 \\ &= 1. \end{align*}$

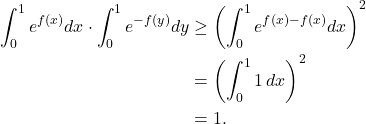
Solution 2

By Jensen’s inequality, since $e^x$ is a convex function, we have

$\int_{0}^{1}e^{f(x)}dx \ge e^{\int_{0}^{1}f(x)dx}$

$\begin{align*}\int_{0}^{1} e^{f(x)} dx \cdot \int_{0}^{1} e^{-f(y)} dy&\geq e^{\int_{0}^{1}f(x)dx}\cdot e^{\int_{0}^{1}-f(x)dx}\\&=e^0\\&=1\end{align*}$

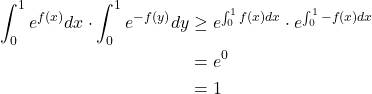
Solution 3

By Hölder’s Inequality, we get

$\int_{0}^{1}\vert u(x)v(x) \vert\leq \left(\int_{0}^{1}\vert u(x)\vert^p dx \right)^{\frac{1}{p}}\left(\int_{0}^{1}\vert u(x)\vert^q dx \right)^{\frac{1}{q}}$

Choose $p=q=2$ , we get the case of solution 1. We can also take $u(x)=e^{f(x)/p}$ and $v(x)=e^{f(x)/q}$ , which would be similar.

Solution 4

Leave a Reply Cancel reply