Let ![]() be a continuous integrable real function on
be a continuous integrable real function on ![]() , then
, then
![]()
Solution 1
By Cauchy-Schwarz inequality,
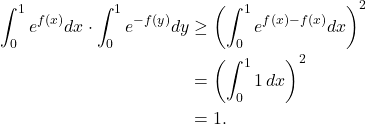
Solution 2
By Jensen’s inequality, since ![]() is a convex function, we have
is a convex function, we have
![]()
So
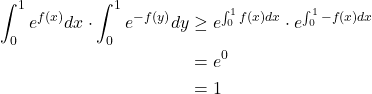
Solution 3
By Hölder’s Inequality, we get
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\vert u(x)v(x) \vert\leq \left(\int_{0}^{1}\vert u(x)\vert^p dx \right)^{\frac{1}{p}}\left(\int_{0}^{1}\vert u(x)\vert^q dx \right)^{\frac{1}{q}}\]](https://zivmaths.com/wp-content/ql-cache/quicklatex.com-21ee0642e2f03fc021e5e7e478953b70_l3.png)
Choose ![]() , we get the case of solution 1. We can also take
, we get the case of solution 1. We can also take ![]() and
and ![]() , which would be similar.
, which would be similar.
Solution 4
Leave a Reply