An approximation problem

June 2026
M	T	W	T	F	S	S
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

Problem: Let us call an irrational number $\alpha \in \mathbb{R}$ well approximated by rational numbers if for any natural numbers $n, N\in \mathbb{N}$ there exists a rational number $p,q$ such that

$\begin{equation*} \vert \alpha -\frac{p}{q}\vert<\frac{1}{Nq^n}\end{equation}$

Construct an example of a well-approximated irrational number.
Prove that a well-approximated irrational number cannot be algebraic, that is, it is transcendental.

Solution:
1. Pick

$\alpha = \sum_{k=1}^{\infty}10^{-k!}$

Why does it work ?

Let’s say we let $\frac{p}{q}=\sum_{k=1}^{m}10^{-k!}$ . Then we have

$\vert \alpha-\frac{p}{q} \vert = \sum_{k=m+1}^{\infty} 10^{-k!}$

and

$\frac{1}{Nq^n}=\frac{1}{N10^{nm!}}$

We now proceed in proving that when $m$ is large enough

$\sum_{k=m+1}^{\infty} 10^{-k!}<\frac{1}{N10^{mk!}}$

We have

$\sum_{k=m+1}^{\infty} 10^{-k!}<10^{(m+1)!}$

So we want

$10^{-(m+1)!} < \frac{1}{N10^{nm!}}$

Since when $m>n$ ,

$10^{-((m+1)!-m(n!))}\leq 10^{-((m+1)!-m!)}<10^{-(m+2)!}$

That means when $10^{(m+2)!}>N$ and $m>n$ , the relationship holds true.

2. This result is a well-known theorem called Liouville’s theorem, you can go to this link for proof.

Our final goal is to understand what causes the difference:
For an algebraic number, if we want to find a rational approximation, then it is inevitable to relation this error with the polynomial, let’s sat $f(x)$ that gives $\alpha$ . Two properties are quite important.

The value 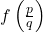$f\left(\frac{p}{q}\right)$ is always a multiple of $\frac{1}{q}$ . This puts restriction on the approximation, as we cannot getting too close with it.
The value

$\frac{\vert f\left(\frac{p}{q}\right)-f(\alpha)\vert}{\vert\frac{p}{q}-\alpha\vert}$

is a bounded value in the vicinity of $\alpha$ . Thus, both conditions put restriction on the approximation, and we cannot have a similar property like transcendental number.

Leave a Reply Cancel reply